[도서] 퀀트의 정석 (1) https://oldnews.tistory.com/393
[도서] 퀀트의 정석 (2) https://oldnews.tistory.com/395
[도서] 퀀트의 정석 (3) https://oldnews.tistory.com/396
[도서] 퀀트의 정석 (4) https://oldnews.tistory.com/435
4장. 자산배분
1. 자산배분
탈무드에서 자산배분을 정수를 얘기하고 있다
"모든 사람으로 하여금 돈을 삼등분하여, 그 돈의 1/3은 땅에, 그 다음 1/3은 사업에, 그리고 나머지 1/3은 손에 쥐고 있게 할지어다"
돈키호테에서도 자산배분의 중요성을 얘기하고 있다.
"계란을 한 바구니에 담지 마라"
자산배분은 수익을 지키는 중요한 도구이다.
2. 상관계수와 분산투자 효과
자산 수익률 변동성
A 4% 10%
B. 6% 14%
위 2개 자산 포트폴리오는 다음 식으로 자산의 수익률과 변동성을 계산할 수 있다.

두 자산 포트폴리오가 수익률과 변동성이 상관계수에 따라 어떻게 변화하는지 수식으로 계산했다.
그림은 상관계수 1은 분산투자 효과가 없음이다. 상관계수가 0은 직선이 아닌 활 모양의 곡선으로 나타난다. 상관계수가 -1은 극단적 수익이 나타난다.

상관계수 1: 분산투자 효과가 없다.
상관계수 0: 활모양 곡선으로 수익률을 낮은 위험(변동성)으로 달성
상관계수 -1: 분산투자 효과 극대화
즉 포트폴리오 안의 자산군 사이의 상관계수가 낮다면 더 높은 수익률을 구현할 수 있다.
대표적 자산 포트폴리오 역의 상관계수를 갖는 자산이 주식과-채권이다. 주식-채권 자산 포트폴리오는 역사적으로 낮은 상관계수를 유지해 오고 있다.

이런 상관관계가 깨지는 경우도 있다.
https://news.einfomax.co.kr/news/articleView.html?idxno=4296433
美 주식·채권 상관관계 깨졌나…2년물 금리·주가 동반 상승 - 연합인포맥스
주식과 채권시장의 상관 관계가 깨졌다는 분석이 나왔다. 통상 2년물 국채금리가 오르면 주가가 하락하는 경향을 보였으나 최근에는 금리가 올라도 주가가 오르는 모습을 보이고 있기 때문이다
news.einfomax.co.kr
다음 그림은 상관계수에 따른 분산투자 효과를 샤프비율 승수로 설명하고있다.
샤프비율 승수는 단일 자산대비 포트폴리오가 얼마나 수익을 내는지에 대한 지표이다.

승수가 2라면 단일 자산대비 포트폴리오가 2배만큼 성과를 낸다는 의미이다.
상관계수가 높다면 자산이 추가되도 샤프비율이 높지 않다.
https://brunch.co.kr/@quantdaddy/110
팩터 상관계수와 분산투자 효과
팩터 포트폴리오의 궁극적인 목표는 당연히 시장의 움직임과 무관하면서도 장기적으로 안정적인 수익을 창출하는 시스템을 만드는 것이다. 이상적인 팩터 포트폴리오를 구성하기 위해 우리에
brunch.co.kr
3. 포트폴리오 이론
상관계수와 포트폴리오에 대한 효과는 1952년 해리 마코워츠에 의해 알려졌다.

마코워츠는 투자 수익률과 위험, 위험회피 성향에 따라 경제적 효용이 결정되는 효용함수를 제시했다.
투자자의 효용 =
기대수익률 - 위험회피성향 x 변동성
투자효과를 위해 기대수익률을 높일 수 있도록 포트폴리오의 변동성을 낮출 수 있는 자산군별 가중치를 찾아야 하고 수익과 위험에서 위험회피성향에 따라 기대수익률이 달라진다.
위험회피성향 과 변동성을 수익률의 가중치로 보면 가중치에 따라 수익률의 변화가 나타난다. 그러므로 위험대비 수익률 가중치를 최적화 하는 방법을 찾아야 포트폴리오 수익률이 극대화 될 수 있다는 의미다.
평균분산 최적화 MVO
위험대비 수익률 가중치를 최적화 하는 방법이 필요한데 보통 "평균-분산 최적화, MVO Mean-variance optimizaiton" 을 사용한다.
https://brunch.co.kr/@quantdaddy/24
평균-분산 최적화, MVO
횡적 리스크 모델 시리즈 #1. | # 포트폴리오 최적화의 시초, 평균-분산 최적화 MVO, 즉 평균-분산 최적화(Mean-Variance Optimization)는 1952년 해리 마코위츠(Harry Markowitz)에 의해 처음 제시되었다. 이 기
brunch.co.kr
MVO 목적함수는 다음 같이 위험회피성향(람다 λ) 과 변동성을 줄여 효용함수를 평균한 것과 비슷하다.
MVO =
기대수익률 - 1/2 x 위험회피성향 x 변동성
MVO 수식 표현
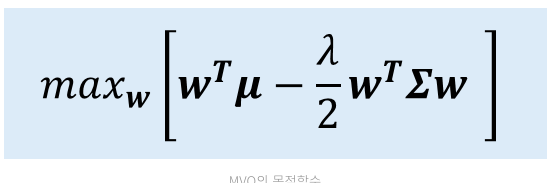
MVO 최적화는 기대수익률과 변동성을 결합한 공분산행렬 계산을 하는데 다음 단계를 거친다.
w가 위험회피성향x변동성인 가중치, u가 기대수익률이고 이 둘의 공분산 행렬 연산을 한다.
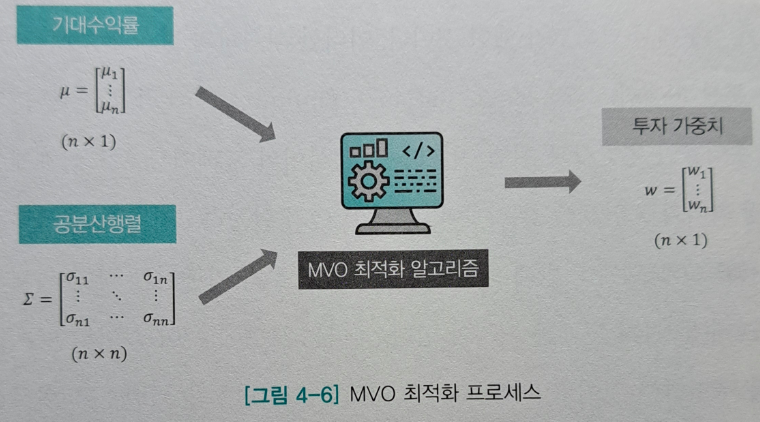
이 결과로 효율적 경계선을 찾는다. 포토폴리오의 모든 경우의 수에서 동일한 위험 대비 가장 높은 수익률을 제공 혹은 동일 수익률 대비 가장 낮은 위험을 제공하는 집합을 연결한 선이다.

4. 포트폴리오와 자본시장선
마코워츠의 포프톨리오 최적화 모델을 결합해 CAPM(Captial Asset Pricing Model) 이론으로 발전했다.
CAMP 목적 함수는
기대수익률 =
무위험 수익률 + 시장민감도 x 시장위험프리미엄
잭 트레이너, 월리엄 샤프, 존 리트너가 제시한 CAPM 자본자산결정모델은 "어던 자산의 기대수익률은 무위험 자산의 수익률에다 위험 자산이 가지고 있는 위험 수준에 대한 기대 보상을 더한것" 이다.
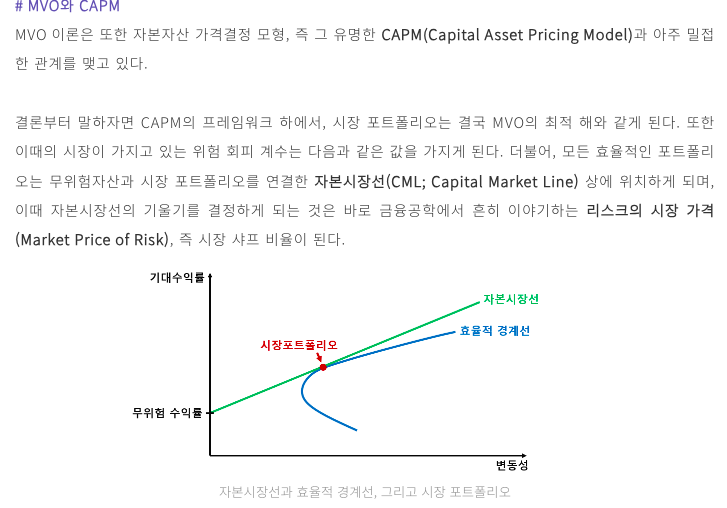
효율적 경계선 밖에 위치한 자산/포트폴리오는 시장 보다 높은 수익률을 보인다. 이런 자산은 저평가/저가격 인 경우다.
효율적 경계선 안에 위치하면 자산/포트폴리오가 과대평가/고가격인 경우로 판단 가능.

5. MVO의 한계
현실적으로 모델에 입력되는 변수가 너무 많다.
자산별 투자 가중치 산출 위해 기대수익률, 변동성 그리고 상관계수의 추정치에 문제가 생기면 가중치가 급격히 변동한다.
그리고 특정 자산에만 가중치가 집중되는 코너(Corner Solution) 현상이 발생한다.
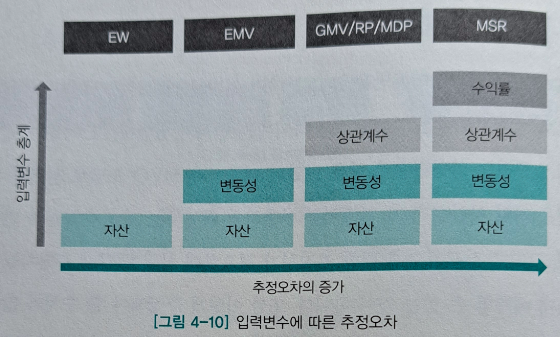
다양한 형태의 최적화 모델이 출현했다.
'Notes' 카테고리의 다른 글
| 논문 읽기 - 방법 요약 (1) | 2024.04.19 |
|---|---|
| [도서] 퀀트의 정석 (4) - 자산배분(2/2) (1) | 2024.04.19 |
| [도서] 월스트리트 퀀트 투자의 법칙 - Part 1 퀀트투자 이해 (0) | 2024.04.08 |
| [도서] 투자도 인생도 복리처럼 - 독서 기억법 (0) | 2024.04.03 |
| [도서] 20대에 시작하는 자산관리 프로젝트 (1) (0) | 2024.04.02 |

댓글